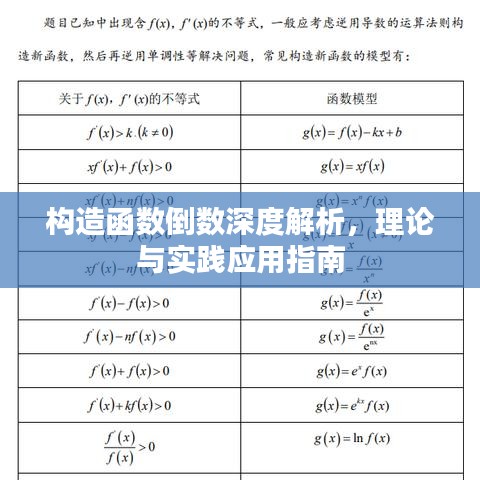
在编程领域，构造函数是一种特殊的方法，用于初始化新创建对象的状态，而倒数则是数学中的一个重要概念，用于描述数列或函数的递减趋势，本文将探讨构造函数与倒数概念的结合，即“构造函数倒数专题”，帮助读者深入理解并实践应用。

构造函数的基本概念

构造函数是一种特殊的成员函数，主要用于初始化对象的状态，在创建对象时，构造函数会自动调用，其主要目的是设置对象的初始状态，确保对象在使用前处于适当的状态。

倒数的概念及其在数学中的应用

倒数是一个数学术语，表示一个数与1的商，在数学中，倒数常用于简化分数、求解方程等，倒数还在其他领域如物理、化学等有着广泛的应用。

构造函数与倒数的结合

在编程中，我们可以将倒数的概念引入到构造函数中，以实现特定的功能，我们可以创建一个表示分数的对象，其中包含一个分子和一个分母，在构造这样的对象时，我们可以使用倒数概念来确保分数的简化形式，还可以利用构造函数来处理一些与倒数相关的运算，如求倒数、倒数相加等。

构造函数倒数专题的实践应用

1、分数类的实现：创建一个分数类，包含分子和分母，在构造函数中，使用倒数概念简化分数，实现加法、减法、乘法、除法等运算方法，这些方法应能处理分子或分母为倒数的特殊情况。

2、求解线性方程：利用构造函数和倒数概念，可以方便地求解线性方程，通过构造矩阵的逆矩阵（即矩阵的倒数），可以求解线性方程组的解。

3、数据结构与算法优化：在数据结构和算法中，利用构造函数处理倒数问题可以提高算法的效率，在堆排序、快速排序等算法中，通过构造特殊的节点结构并利用倒数概念进行优化，可以提高算法的性能。

注意事项与常见问题解决方案

1、精度问题：在处理倒数时，需要注意精度问题，可以使用高精度库或自定义数据类型来确保计算的准确性。

2、除数为零问题：在处理倒数时，需要特别注意除数为零的情况，可以通过异常处理机制来避免程序崩溃。

3、性能优化：在处理复杂的数据结构和算法时，需要注意性能优化，可以通过选择合适的算法和数据结构、利用缓存等手段来提高性能。

本文详细探讨了“构造函数倒数专题”，包括构造函数和倒数的基本概念、二者的结合及其在编程中的应用，通过实践应用示例和注意事项，读者可以更好地理解并应用构造函数倒数专题解决实际问题，希望本文能对读者在编程和数学领域的学习和实践有所帮助。

展望

随着计算机科学的不断发展，构造函数倒数专题的应用将更加广泛，在机器学习、深度学习等领域，可以利用构造函数处理倒数问题来提高模型的性能和准确性，随着新型数据结构和算法的出现，构造函数倒数专题将在更多领域发挥重要作用。